Alejandro Bernardin, Haochuan Chen, Jeffrey R. Comer, Giacomo Fiorin, Haohao Fu, Jérôme Hénin, Axel Kohlmeyer, Fabrizio Marinelli, Joshua V. Vermaas, Andrew D. White

(PDF version)

Contents

In molecular dynamics simulations, it is often useful to reduce the large number of degrees of freedom of a physical system into few parameters whose statistical distributions can be analyzed individually, or used to define biasing potentials to alter the dynamics of the system in a controlled manner. These have been called ‘order parameters', ‘collective variables', ‘(surrogate) reaction coordinates', and many other terms.

Here we use primarily the term ‘collective variable', often shortened to colvar, to indicate any differentiable function of atomic Cartesian coordinates, $x_i$, with $i$ between $1$ and $N$, the total number of atoms:

This manual documents the collective variables module (Colvars), a software that provides an implementation for the functions $\xi \left(X\right)$ with a focus on flexibility, robustness and high performance. The module is designed to perform multiple tasks concurrently during or after a simulation, the most common of which are:

• apply restraints or biasing potentials to multiple variables, tailored on the system by choosing from a wide set of basis functions, without limitations on their number or on the number of atoms involved;
• calculate potentials of mean force (PMFs) along any set of variables, using different enhanced sampling methods, such as Adaptive Biasing Force (ABF), metadynamics, steered MD and umbrella sampling; variants of these methods that make use of an ensemble of replicas are supported as well;
• calculate statistical properties of the variables, such as running averages and standard deviations, correlation functions of pairs of variables, and multidimensional histograms: this can be done either at run-time without the need to save very large trajectory files, or after a simulation has been completed (post-processing).

Note: although restraints and PMF algorithms are primarily used during simulations, they are also available in VMD to test a new input for a simulation, or to evaluate the relative free energy of a new structure based on data from a previous calculation. Options that only have an effect during a simulation are also included for compatibility purposes.

Detailed explanations of the design of the Colvars module are provided in reference [1]. Please cite this reference whenever publishing work that makes use of this module, alongside any other publications for specific features being, according to the usage summary printed when running a Colvars-enabled MD simulation or analysis.

Using the Colvars module in VMD Within VMD [2], the Colvars module can be accessed in two ways:

• Using the Colvars Dashboard, an intuitive interface to the Colvars module, to easily define and analyze collective variables, but not biases (section 3).
• Using the full-featured Tcl scripting interface as documented in section 4.2; see in particular the example in section 4.2.5.

The Colvars configuration is a plain text file or string that defines collective variables, biases, and general parameters of the Colvars module. It is passed to the module using back-end-specific commands documented in section 4. Writing the configuration fora collective variable in VMD is made much easier using the Dashboard and its configuration editor (section 3). However, note that the Dashboard does not handle biases: if necessary, they should be managed separately using the scripting interface.

Example: steering two groups of atoms away from each other. Now let us look at a complete, non-trivial configuration. Suppose that we want to run a steered MD experiment where a small molecule is pulled away from a protein binding site. In Colvars terms, this is done by applying a moving restraint to the distance between the two objects. The configuration will contain two blocks, one defining the distance variable (see section 5 and 5.2.1), and the other the moving harmonic restraint (7.5). Note that in VMD, no biasing forces are applied, but biases may be useful in the context of an analysis script, e.g. to collect histograms or to compute bias energies.

colvar {
  name dist
  distance {
    group1 { atomNumbersRange 42-55 }
    group2 {
      psfSegID  PR
      atomNameResidueRange  CA 15-30
    }
  }
}

harmonic {
  colvars dist
  forceConstant 20.0
  centers 4.0         # initial distance
  targetCenters 15.0  # final distance
  targetNumSteps 500000
} 

Reading this input in plain English: the variable here named dist consists in a distance function between the centers of two groups: the ligand (atoms 42 to 55) and the $\alpha$-carbon atoms of residues 15 to 30 in the protein (segment name PR). To the “dist" variable, we apply a harmonic potential of force constant 20 energy unit/length unit${}^2$, initially centered around a value of 4 length unit, which will increase to 15 length unit over 500,000 simulation steps.

The atom selection keywords are detailed in section 6.

Example: using multiple variables and multiple biasing/analysis methods together. A more complex example configuration is included below, showing how a variable may be constructed by combining multiple existing functions, and how multiple variables or multiple biases may be used concurrently. The colvar indicated below as “$d$" is defined as the difference between two distances (see 5.2): the first distance ($d_1$) is taken between the center of mass of atoms 1 and 2 and that of atoms 3 to 5, the second ($d_2$) between atom 7 and the center of mass of atoms 8 to 10 (see 6). The difference $d=d_1-d_2$ is obtained by multiplying the two by a coefficient $C=+1$ or $C=-1$, respectively (see 5.16). The colvar called “$c$" is the coordination number calculated between atoms 1 to 10 and atoms 11 to 20. A harmonic restraint (see 7.5) is applied to both $d$ and $c$: to allow using the same force constant $K$, both $d$ and $c$ are scaled by their respective fluctuation widths $w_d$ and $w_c$. A third colvar “alpha" is defined as the $\alpha$-helical content of residues 1 to 10 (see 5.7.1). The values of “$c$" and “alpha" are also recorded throughout the simulation as a joint 2-dimensional histogram (see 7.10).

colvar {
  # difference of two distances
  name d 
  width 0.2 # estimated fluctuation width 
  distance {
    componentCoeff 1.0
    group1 { atomNumbers 1 2 }
    group2 { atomNumbers 3 4 5 }
  }
  distance {
    componentCoeff -1.0
    group1 { atomNumbers 7 }
    group2 { atomNumbers 8 9 10 }
  }
}

colvar {
  name c
  coordNum {
    cutoff 6.0
    group1 { atomNumbersRange 1-10 }
    group2 { atomNumbersRange 11-20 }
    tolerance 1.0e-6
    pairListFrequency 1000
  }
}
colvar {
  name alpha
  alpha {
    psfSegID PROT
    residueRange 1-10
  }
} 
harmonic {
  colvars d c
  centers 3.0 4.0
  forceConstant 5.0
}

histogram {
  colvars c alpha
} 

The Colvars Dashboard is a graphical interface for interactive visualization and refinement of collective variables aided by molecular structures and trajectories. It is accessible in VMD's Main Menu under “Extensions/Analysis/Colvars Dashboard". Throughout the interface, keyboard shortcuts for common operations are indicated in square brackets. Context menus in the colvar and bias tables can be accessed using either right click or Control-click.

Here are the steps for a quick first tour of the Dashboard:

1. load an MD trajectory into VMD;
2. open the Dashboard;
3. click “New" to create a new collective variable;
4. in the Editor window, click “Apply" to accept the default template;
5. in the Dashboard window, click “Show atoms" to display the two atom groups involved in this distance coordinate;
6. click “Timeline plot";
7. click anywhere in the timeline plot to navigate in the trajectory.

Alternately, use the Automatic colvars features in the Actions tab.

Now, clicking “Edit" in the Dashboard window (or right-clikcing on a colvar in the list view), you can modify the collective variable to reflect interesting geometric properties of the system. The power of the collective variables approach lies in the variety of geometric functions (“components") and their combinations. The editor window provides a number of helpers to make it easy and quick to define the most relevant variables. See section 3.5 for details.

The Dashboard window displays a table listing currently defined variables, and their values for the current frame indicated at the bottom of the window. By default the frame is updated to track VMD's currently displayed frame, but that can be changed by toggling the “Track frame" checkbox, e.g. to animate the trajectory without recomputing expensive variables. Vector-values variables can be expanded to list their scalar elements. This is necessary when individual scalar quantities have to be selected for plotting. Other operations act on variables as a whole and ignore specific selected scalar elements. Right-clicking in the table brings up a context menu with specific actions for the selected variables.

Buttons above the table allow for general operations on the state of the Colvars module. Below the table, the Actions tab allows operations on selected variables, while the Settings tab offers advanced settings for the various visualizations.

If variables are modified, added or deleted by an external script, hit “Refresh" or press F5 to update the displayed variables and values. Starting the Dashboard also enables trajectory animation using the left/right arrow keys within VMD's graphical window. Atomic coordinates can be modified using VMD's “Mouse/Move" functions, and the Colvars module can then be updated by pressing F5 directly from the graphical window.

A dropdown list allows for changing the current unit system if no variables are defined (see section 4.1). When changing units, it is strongly recommended to check the configuration for all colvars to ensure that all quantities are expressed in the desired set of units.

The Colvars Module interacts with one VMD Molecule at a time. At the bottom of the Actions tab, a dropdown lets the user change which VMD molecule is associated with the Colvars module. Internally, changing it means recording the configuration of currently defined colvars, deleting the current instance of the Colvars module, creating a new one linked to the target molecule, and applying the saved configuration. Beware of incompatible colvar definitions, such as atom groups listing atom IDs that exist in one molecule, but not the other. Auto-updating selections (see below) can be used to adapt the colvar definitions to a different system using VMD selection texts.

This saves the current configuration of the colvars Module to a file. This includes comments found in the input, general parameters of the Colvars Module, the collective variables themselves, and collective variable biases. The resulting configuration file can be read by Colvars, either back in VMD, or within a supported MD engine.

The Actions tab offers two buttons to generate sets of colvars from the current VMD session:

• "protein auto-colvars" creates variables describing classic quantities used to describe protein structures;
• "colvars from VMD labels" creates variables based on visible labels (Bonds, Angles, Dihedrals) for the current molecule (see Molecule selector in the same tab). Such labels can be created by setting the label mode with the key 2, 3, or 4, and picking atoms with the mouse.

These automatically generated colvars can be used as-is, or customized using the configuration editor (Edit in the context menu, or in the Actions tab).

The configuration editor can be started with the “Edit" or “New" buttons. Using the “Edit" button, the configuration of selected variables is loaded, and those variables will be replaced when applying the new configuration.

The editor window offers links to online documentation, as well as helpers to write correct configuration files.

As a first step, the most useful helper is the collection of template files. Some parameters that must be supplied are indicated by the symbol @. Colvar templates can be inserted at the beginning of the configuration, whereas “component" templates define basis functions that belong inside a colvar block. Templates are indented using 4 spaces per level to indicate their position in the nested structure of the configuration: general options, colvars and biases at level 0, bias and colvar parameters like components at level 1, component parameters such as atom groups at level 2, and atom group parameters at level 3.

The next helper buttons allow importing atom selections from VMD, either typing a VMD atom selection text, by copying the selection of an existing graphical representation, or by inserting the list of atoms currently labeled in VMD using the “Pick atom" feature. Atom selections should be inserted within an atom group block, within a component block (such as distance). By default atom selections are preceded with a comment line marking them as auto-updating. This instructs the Dashboard to update the list of atoms whenever the configuration is applied, that is, when it is edited, when the file is loaded by the Dashboard, or when changing the VMD molecule linked to Colvars. This is useful when working across systems with different atom numberings, but topologies that make the relevant atom groups identifiable using VMD selection texts. Special fields (O, B, and user) may be used, as well as atom positions (e.g. z > 0). If the selection text is modified manually, the atom list will be updated when applying the new configuration. This auto-updating behavior can be disabled by removing the special comment line or altering the keywords “auto-updating selection".

Note that atom lists are not auto-updated:

1. when changing frame within the same molecule (animating a trajectory);
2. when the configuration is read by the Colvars module outside of VMD (eg. within an MD engine).

The “Insert labeled..." button combined with the selection box allows for inserting components matching VMD's geometry measurements: Bonds (distances), angles, and dihedrals. Hidden labels are not used for inserting components.

Timeline plots show the selected variables as a function of time. A vertical bar indicates the current frame, which can be changed either using VMD's trajectory animation controls, or directly in the plot window by clicking the mouse inside the graph, or using the keyboard left/right arrows. Shift+arrow steps by 10 frames for faster animation, and Ctrl+arrow steps over 50 frames. The Home/End keys jump to the first and last frames, respectively. The up/down arrows operate a zoom/unzoom along the time axis. Visible data can be fitted vertically using the h key. All data can be fitted horizontally using the h key.

Pairwise scatterplots are useful to identify correlation between variables. To create a pairwise plot, select exactly two scalar variables (or scalar components of vector variables), and click “Pairwise plot". Frames are represented by circles, and lines connect consecutive frames. The blue dot tracks the current frame: clicking a circle jumps to the corresponding frame. Arrow keys and Home/End animate the trajectory as in the timeline plot.

Histogram displays a histogram of the selected scalar variable over the trajectory, using approximately the number of bins specified in the Settings tab (adjusted after selecting a round number for the bin width). The current value of the colvar is indicated by a vertical bar. Clicking anywhere in the plot jumps to the frame with the nearest value of the colvar. Keyboard navigation of the trajectory is similar to the other plots, except that the trajectory is traversed according to colvar values rather than frame numbers. This enables exploration of frames corresponding to a neighborhood of colvar values, even when they are not contiguous in time.

“Show atoms" creates representations of the atoms involved in the definition of the selected colvars. Each atom group is shown in a different color. “Show gradient" is available for scalar variables only. It creates a graphical representation of the atomic gradients of the selected variables, visualizing how the value of the collective variable would vary in response to a change in atomic coordinates. The graphical representation of the gradients is controlled by parameters in the Settings tab. Vectors representing the gradient are rescaled as indicated by the radio buttons Max. vector norm and Scaling factor. Max. vector norm rescales gradients so that the largest vector component of each colvar's gradient is represented by an arrow of the specified length, in Å. Scaling factor rescales gradients by the specified factor, divided by the colvar's width parameter (1 by default, see 5.19). This use of width makes it easier to compare the gradients of collective variables that are not commensurate. The scaling factor has the unit $\ast L∕(cv∕width)$, where $L$ is the current length unit, and $cv$ represents the natural unit of the collective variable. By default $width$ is unity, but $(cv∕width)$ may be seen as dimensionless if $width$ is expressed in cv units.

The Dashboard offers visualizations for specific types of variables:

• Variables that represent rotation operations (as unit quaternions), such as those based on an orientation component, can be displayed by right-clicking on them in the colvar table. This creates a representation of the rotation as an arrow representing its axis, and two arms separated by the angle of the rotation, between 0 and 180 degrees.
• For variables that are computed based on volumetric maps, representations of the related maps can be created using the "Show volmap" button, or again through a specific entry in the context menu available via right-click.

Parameters for fine-tuning these visualizations can be set in the Settings tab.

The main Dashboard window features a "Biases" tab that contains a list of currently defined biases, their current energy, and the colvars that they depend upon. A new harmonic bias acting on a given set of colvars can be created by selecting the colvars and opening the context menu in the colvar table (right click or control-click). A button enables creating a Timeline plot with the energies of currently selected biases, similar to the colvar Timeline plot. Only one plot can be active at a time. Another button creates a visualization of the biasing forces computed by the selected biases, similar to the gradient display for colvars. The graphical representation of forces is controlled by the same parameters as the gradients, shown in the Settings tab. The difference is the scaling factor unit, which is Ångström per Colvars force unit (that is, Ångström times Colvars length unit per Colvars energy unit).

Note that the energy of history-dependent biases such as ABF or metadynamics may not be updated in VMD. However, values of the bias energy from a previous simulation can be displayed if a state file has been loaded with cv load (section 4.2), or in the case of ABF, if inputPrefix was specified.

Hitting the Save button will save the configuration of any bias listed in this tab, except the harmonic wall biases that are created automatically from a colvar for which the lower or upper wall options are specified.

Sometimes, important time-dependent quantities are available for a trajectory, but must be computed by an external tool (e.g. energies from a simulation). These can be visualized alongside colvars by taking advantage of the scripted colvar feature.

Such a custom variable can either be computed on the fly (by calling an external tool or a VMD feature) or pre-computed and cached. For example, we can use VMD to compute the protein solvent-accessible surface area (SASA) on the fly:

set sasa_sel [atomselect top "protein and noh"]

proc calc_user_colvar { x } {
  # Follow current Colvars frame
  $::sasa_sel frame [cv frame]
  return [measure sasa 1 $::sasa_sel]
} 

The Tcl script above should be entered into VMD's text console, or sourced from a file. Then we can define a colvar that will be calculated by the scripted procedure above, by entering the following configuration as a new colvar in the Dashboad Editor Window:

colvar {
    name user
    scriptedFunction user_colvar
    distance {
        # The distance component is just a placeholder
        group1 {
            dummyatom (0, 0, 0)
        }
        group2 {
            dummyatom (0, 0, 0)
        }
    }
} 

If the SASA computation is slow, it can be cached to make subsequent interaction responsive. To that effect, we source the following script to pre-compute the SASA for every frame and store it in VMD's User field for atom 0.

set atom0_sel [atomselect top "index 0"]

for {set f 0} {$f < [molinfo top get numframes]} {incr f} {
  $::sasa_sel frame $f
  $::atom0_sel frame $f
  $::atom0_sel set user [measure sasa 1 $::sasa_sel]
} 

Then we use the following Tcl procedure to compute a custom variable that is simply equal to the User field for atom 0 for the current frame:

proc calc_user_colvar { x } {
  # Follow current Colvars frame
  $::atom0_sel frame [cv frame]
  return [$::atom0_sel get user]
} 

This version results in extremely fast updates.

Here, we document the syntax of the commands and parameters used to set up and use the Colvars module in VMD. One of these parameters is the configuration file or the configuration text for the module itself, whose syntax is described in 4.3 and in the following sections.

The “internal units" of the Colvars module are the units in which values are expected to be in the configuration file, and in which collective variable values, energies, etc. are expressed in the output and colvars trajectory files. Generally the Colvars module uses internally the same units as its back-end MD engine, with the exception of VMD, where different unit sets are supported to allow for easy setup, visualization and analysis of Colvars simulations performed with any simulation engine.

Note that angles are expressed in degrees, and derived quantites such as force constants are based on degrees as well. Some colvar components have default values, expressed in Ångström in this documentation. They are converted to the current length unit as needed. Atomic coordinates read from XYZ files (and PDB files where applicable) are expected to be expressed in Ångström, no matter what unit system is in use by the back-end (VMD) or the Colvars Module. They are converted internally to the current length unit as needed. Note that force constants in harmonic and harmonicWalls biases (7.5) are rescaled according to the width parameter of colvars, so that they are formally in energy units, although if width is given its default value of 1.0, force constants are effectively expressed in energy unit/(colvar unit)${}^2$.

To avoid errors due to reading configuration files written in a different unit system, it can be specified within the input:

• Keyword units$⟨$Unit system to be used$⟩$
  Context: global
  Acceptable values: string
  Description: A string defining the units to be used internally by Colvars. Supported values are: real (Å, kcal/mol), gromacs (nm, kJ/mol), metal (Å, eV), and electron (Bohr, Hartree). In VMD, the default system of units for Colvars is VMD's native units: real (Å, kcal/mol). However, the units keyword will switch to a different unit system than the current one if no colvars were defined before reading the current configuration. If colvars are already defined, units will refuse changing the unit system to avoid making the definition of those variables erroneous in the new system of units. If needed this precaution can be overridden using the cv units scripting command (4.2).

After the first initialization of the Colvars module, the internal state of Colvars objects may be queried or modified in a VMD script:

cv $<$method$>$ arg1 arg2 ...

where $<$method$>$ is the name of a specific procedure and arg1, arg2, …are its required and/or optional arguments.

In VMD, the cv command is used by the Dashboard graphical interface,(3), but can be also used in scripts or interactively from the command-line terminal (for example, in remote terminal sessions) or in the Tk Console.

In the remainder of this section, the most frequently used commands of the Colvars scripting interface are discussed and exemplified. For a full list of scripting commands available, see section 8.

The first step to using Colvars in VMD is choosing which “molecule" (i.e. which system): because VMD can handle multiple “molecules", the Colvars module needs to remain attached to a specific VMD molecule. For example:

cv molid "top" 

will attach the Colvars module onto the molecule currently holding the “top" status (alternatively, you can refer to a molecule by its numeric ID in lieu of top). All following invocations of the cv command will continue operating on the same molecule, regardless of whether other molecules are loaded, or which one has the “top" status. The cv molid command without argument will return the molid currently associated with Colvars.

To define new collective variables and/or biases for immediate use in the current session, configuration can be loaded from an external configuration file:

cv configfile "colvars-file.in" 

This can in principle be called at any time, if only flags internal to Colvars are being modified. In practice, when new atoms or any new atomic properties (e.g. total forces) are being requested, initialization steps will be required that are not carried out during a simulation. Therefore, it is generally good practice in a simulation to change the Colvars configuration outside the scope between segments of the same computation. However, in VMD initialization is always immediate, allowing interactive usage by Tcl scripts or the Dashboard.

To load the configuration directly from a string the “config" method may be used:

cv config "keyword { ... }" 

The vast majority of the syntax in Colvars is backward-compatible, adding keywords when new features are introduced. However, when using multiple versions simultaneously it may be useful to test within the script whether the version is recent enough to support the desired feature. The “version" can be used to get the Colvars version for this use:

 if { [cv version] >= "2020-02-25" } {
  cv config "(use a recent feature)"
} 

After a configuration is fully defined, the “load" method may be used to load a state file from a previous simulation that contains e.g. data from history-dependent biases), to either continue that simulation or analyze its results:

cv load "$<$oldjob$>$.colvars.state"

or more simply using the prefix of the state file itself:

cv load "$<$oldjob$>$"

The “save" method, analogous to “load", allows to save all restart information to a state file. This is normally not required during a simulation if colvarsRestartFrequency is defined (either directly or indirectly by the VMD restart frequency). Because not only a state file (used to continue simulations) but also other data files (used to analyze the trajectory) are written, it is generally recommended to call the save method using a prefix, rather than a complete file name:

cv save "$<$job$>$"

For computational efficiency the Colvars module keeps internal copies of the numeric IDs, masses, charges, positions, and optionally total forces of the atoms requested for a Colvars computation. At each simulation step, up-to-date versions of these properties are copied from the central memory of VMD into the internal memory of the Colvars module. In a post-processing workflow or outside a simulation (e.g. when using VMD), this copy can be carried out as part of the update method:

cv update   

which also performs the (re-)computation of all variables and biases defined in Colvars.

For example, the current sequence of numeric IDs of the atoms processed by Colvars can be obtained as:

cv getatomids   

and their current positions as:

cv getatompositions   

This may prove useful to test the correctness of the coordinates passed to Colvars, particularly in regard to periodic boundary conditions (6.3). There is currently no mechanism to modify the above fields via the scripting interface, but such capability will be added in the future.

While running a simulation, or when setting one up in VMD, it is possible to examine all the forces that were last applied by Colvars to the atoms, or are about to be applied:

cv getatomappliedforces   

where the length and order of this sequence matches that provided by the getatomids method. A simpler way of testing the stability of a Colvars configuration before or during a simulation makes use of aggregated data, such as the energy:

cv getenergy   

the root-mean-square of the Colvars applied forces:

cv getatomappliedforcesrms   

or the maximum norm of the applied forces:

cv getatomappliedforcesmax   

which can be matched to a specific atom via its numeric ID obtained as:

cv getatomappliedforcesmaxid   

See 8.1 for a complete list of scripting commands used to manage atomic data and runtime parameters of the Colvars module.

One of the typical uses of Colvars in VMD is computing the values of one or more variables along an existing trajectory. This is most easily done using the Dashboard (section 3), but can also be done by a script, as in the example below:

# Activate the module on the current VMD molecule
cv molid top
# Load a Colvars config file
cv configfile test.in
set out [open "test.colvars.traj" "w"]
# Write the labels to the file
puts -nonewline ${out} [cv printframelabels]
for { set fr 0 } { ${fr} < [molinfo top get numframes] } { incr fr } {
  # Point Colvars to this trajectory frame
  cv frame ${fr}
  # Recompute variables and biases (required in VMD)
  cv update
  # Print variables and biases to the file
  puts -nonewline ${out} [cv printframe]
}
close ${out} 

After one or more collective variables are defined, they can be accessed with the following syntax.

 cv colvar "$<$name$>$" $<$method$>$ arg1 arg2 ...

where “$<$name$>$" is the name of the variable.

For example, to recompute the collective variable “xi" after a change in its parameters, the following command can be used:

 cv colvar "xi" update  

This ordinarily is not needed during a simulation run, where all variables are recomputed at every step (along with biasing forces acting on them). However, when analyzing an existing trajectory, e.g. in VMD, a call to update is generally required.

While in all typical cases all configuration of the variables is done with the “config" or “configfile" methods, a limited set of changes can be enacted at runtime using:

 cv colvar "$<$name$>$" modifycvcs arg1 arg2 ...

where each argument is a string passed to the function or functions that are used to compute the variable, and are called colvar components, or CVCs (5.1). For example, a variable “DeltaZ" made of a single “distanceZ" component can be made periodic with a period equal to the unit cell dimension along the $Z$-axis:

 cv colvar "DeltaZ" modifycvcs "period ${Lz}" 

Please note that this option is currently limited to changing the values of the polynomial superposition parameters componentCoeff, or of the componentExp to update on the fly, of period, wrapAround or forceNoPBC options for components that support them.

If the variable is computed using many components, it is possible to selectively turn some of them on or off:

 cv colvar "$<$name$>$" cvcflags $<$flags$>$

where “$<$flags$>$" is a list of 0/1 values, one per component. This is useful for example when script-based path collective variables in Cartesian coordinates (5.10.3) are used, to minimize computational cost by disabling the computation of terms that are very close to zero.

Important: None of the changes enacted by the “modifycvcs" or “cvcflags" methods will be saved to state files, and will be lost when restarting a simulation, deleting the corresponding collective variable, or resetting the module with the “delete" or “reset" methods.

As soon as a colvar “xi" and its associated biasing potentials are up to date (i.e. during a MD run, or after the respective “update" methods have been called), the force applied onto the colvar is known and may be accessed through the getappliedforce method:

 cv colvar "xi" getappliedforce  

See also the use of the outputAppliedForce option to have this force be saved to file during a simulation.

Aside from the biasing methods already implemented within Colvars (7) this force may be incremented ad hoc, for example as part of a custom restraint implemented by scriptedColvarForces:

 cv colvar "xi" addforce $<$force$>$

where “$<$force$>$" is a scalar or a vector (depending on the type of variable “xi"). Note that in VMD, any forces applied via addforce do not have any effect on the movement of atoms: this feature is only available for compatibility.

For certain types of variable, the force applied directly on a colvar may be combined with those acting indirectly on it via the interatomic force field, making up the total force. When the outputTotalForce kewyord is enabled, or when a biasing method that makes explicit use of the total force is enabled, the total force may be obtained as:

 cv colvar "xi" gettotalforce  

Note that not all types of variable support total-force computation, and the value of the total force may not be available immediately within the same simulation step: see the documentation of outputTotalForce for more details.

See 8.2 for a complete list of scripting commands used to manage collective variables.

Because biases depend only upon data internal to the Colvars module (i.e. they do not need atomic coordinates from VMD), it is generally easy to create them or update their configuration at any time. For example, given the most current value of the variable “xi", an already-defined harmonic restraint on it named “h_xi" can be updated as:

 cv bias "h_xi" update  

During a running simulation this step is not needed, because an automatic update of each bias is already carried out.

Some types of bias are history-dependent, and the magnitude of their forces depends not only on the values of their corresponding variables, but also on previous simulation history. It is thus useful to load information from a state file that contains information specifically for one bias only, for example:

 cv bias "metadynamics1" load "old.colvars.state" 

or alternatively, using the prefix of the file instead of its full name:

 cv bias "metadynamics1" load "old" 

A corresponding “save" function is also available:

 cv bias "metadynamics1" save "new" 

This pair of functions is also used internally by Colvars to implement e.g. multiple-walker metadynamics (7.4.7), but they can be called from a scripted function to implement alternative coupling schemes.

See 8.3 for a complete list of scripting commands used to manage biases.

Configuration for the Colvars module is passed using an external file, or inlined as a string in a VMD script using the Tcl command cv config "...". Configuration lines follow the format “keyword value" or “keyword { ... }", where the keyword and its value must be separated by one or more space characters. The following formatting rules apply:

• Keywords are case-insensitive; for example, upperBoundary is the same as upperboundary and UPPERBOUNDARY); note that their string values are however still case-sensitive (e.g. names of variables, file names).
• A long value, or a list of multiple values, can be distributed across multiple lines by using curly braces, “{" and “}": the opening brace “{" must occur on the same line as the keyword, following at least one space character; the closing brace “}" may be at any position after that; any keywords following the closing brace on the same line are not valid (they should appear instead on a different line).
• Many keywords are nested, and are only meaningful within the specific context of another keyword; for example, the keyword name is available inside the block of the keyword colvar {...}, but not outside of it; for every keyword documented in the following, the “parent" keyword that defines such context is also indicated.
• If a keyword requiring a boolean value (yes|on|true or no|off|false) is provided without an explicit value, it defaults to ‘yes|on|true'; for example, ‘outputAppliedForce' may be used as shorthand for ‘outputAppliedForce on'.
• The hash character “#" indicates a comment: all text in the same line following this character will be ignored.
• Outside of comments, only ASCII characters are allowed for defining keywords, and the only white-space characters supported are spaces, tabs and newlines: a warning will be printed upon detection of non-ASCII characters in a configuration line, which include both characters that are visibly “special", as well as those with a very similar appearance to ASCII ones (for instance, non-breaking spaces); common ways to identify/remove non-ASCII characters are using the Emacs text editor, or using LC_ALL=C vi.
• Tcl syntax is generally not available inside a Colvars configuration file/string, but it is possible to use Tcl variables or bracket expansion of commands when configuration is passed via the command cv config "..."; for example, it is possible to convert the atom selection $sel into an atom group (see 6.1) using cv config "atomNumbers { [$sel get serial] }".

The following keywords are available in the global context of the Colvars configuration, i.e. they are not nested inside other keywords:

•   Keyword colvarsTrajFrequency$⟨$Colvar value trajectory frequency$⟩$
  Context: global
  Acceptable values: positive integer
  Default value: 100
  Description: The values of each colvar (and of other related quantities, if requested) are written to the file outputName.colvars.traj every these many steps throughout the simulation. If the value is 0, such trajectory file is not written. For optimization the output is buffered, and synchronized with the disk only when the restart file is being written.
•   Keyword colvarsRestartFrequency$⟨$Colvar module restart frequency$⟩$
  Context: global
  Acceptable values: positive integer
  Default value: 0
  Description: The state file and any other output files produced by Colvars are written every these many steps (the trajectory file is still written every colvarsTrajFrequency steps). In VMD, the simulation step is not progressed and this parameter is effectively ignored. It is generally a good idea to leave this parameter at its default value, unless needed for special cases or to disable automatic writing of output files altogether. Writing can still be invoked at any time via the command cv save.
•   Keyword indexFile$⟨$Index file for atom selection (GROMACS “ndx" format)$⟩$
  Context: global
  Acceptable values: UNIX filename
  Description: This option reads an index file (usually with a .ndx extension) as produced by the make_ndx tool of GROMACS. This keyword may be repeated to load multiple index files. A group with the same name may appear multiple times, as long as it contains the same indices in identical order each time: an error is raised otherwise. The names of index groups contained in this file can then be used to define atom groups with the indexGroup keyword. Other supported methods to select atoms are described in 6.
•   Keyword smp$⟨$Whether SMP parallelism should be used$⟩$
  Context: global
  Acceptable values: boolean
  Default value: on
  Description: If this flag is enabled (default), SMP parallelism over threads will be used to compute variables and biases, provided that this is supported by the VMD build in use.

A state file contains the information produced during a Colvars-based simulation besides atomic data, which is provided by VMD.

Because many of the methods implemented in Colvars are history-dependent, this file is often needed to continue a long simulation over consecutive runs. Such state file is written automatically at the end of any simulation with Colvars, and contains data accumulated during that simulation along with the step number at the end of it. The step number read from the state file is then used to control such time-dependent biases: because of this essential role, the step number internal to Colvars may not always match the step number reported by the MD program that carried during the simulation (which may instead restart from zero each time).

Depending on the configuration, a state file may need to be loaded issued at the beginning of a new simulation when time-dependent biasing methods are applied (moving restraints, metadynamics, ABF, ...). . After initialization of the Colvars module, a state file may be loaded at any time with the Tcl command cv load.

It is possible to load a state file even if the configuration has changed: for example, new variables may be defined or restraints be added in between consecutive runs. For each newly defined variable or bias, no information will be read from the state file if this is unavailable: such new objects will remain uninitialized until the first compute step. Conversely, any information that the state file has about variables or biases that are no longer defined is silently ignored. Because these checks are performed based on the names of variables and biases, it is the user's responsibility to ensure that these definitions are consistent between runs.

During a simulation with collective variables defined, the following three output files are written:

• A state file, named outputName.colvars.state; this file is in ASCII (plain text) format. This file is written at the end of the specified run, but can also be written at any time with the command cv save (4.2.3).
  This is the only Colvars output file needed to continue a simulation.
• If the parameter colvarsRestartFrequency is larger than zero, a restart file is written every that many steps: this file is fully equivalent to the final state file. The name of this file is restartName.colvars.state.
• If the parameter colvarsTrajFrequency is greater than 0 (default value: 100 steps), a trajectory file, named outputName.colvars.traj, is written during the simulation. Unlike the state file, this file is not needed to restart a simulation, but can be used for post-processing and analysis. The format of this file is described in sec. 4.7.6.
• Additionally, certain features, when enabled, can emit output files with a specific purpose: for example, potentials of mean force can be written to file to be analyzed or plotted. These files are described in the respective sections, but as a general rule they all use names beginning with the outputNameprefix.

Other output files may also be written by specific methods, e.g. the ABF or metadynamics methods (7.2, 7.4). Like the trajectory file, they are needed only for analyzing, not continuing a simulation. All such files' names also begin with the prefix outputName.

This section summarizes the file formats of various files that Colvars may be reading or writing.

Configuration files are text files that are generally read as input by VMD, and may be optionally inlined in a VMD script (see 4.2.1). Starting from version 2017-02-01, changes in newline encodings are handled transparently, i.e. it is possible to typeset a configuration file in Windows (CR-LF newlines) and then use it with Linux or macOS (LF-only newlines).

State files, although not written manually, follow otherwise the same text format as configuration files.

For atom selections that cannot be specified only by using internal Colvars keywords, external index files may also be used following the NDX format used in GROMACS:

[ group_1_name ]
  i1  i2  i3  i4  ...
  ...             ...  iN
[ group_2_name ]
  ... 

where i1 through iN are 1-based indices. Each group name may not contain spaces or tabs: otherwise, a parsing error will be raised.

Multiple index files may be provided to Colvars, each using the keyword indexFile. Two index files may contain groups with the same names, however these must also represent identical atom selections, i.e. the same sequence of indices including order.

Other than with GROMACS, an index group may also be generated from the VMD command-line interface, using the helper function write_index_group provided in the colvartools folder:

source colvartools/write_index_group.tcl
set sel [atomselect top "resname XXX and not hydrogen"]
write_index_group indexfile.ndx $sel "Ligand" 

where $N$ is the number of atomic coordinates in the file and $E_i$ is the chemical element of the $i$-th atom. Because $E_i$ is not used in Colvars, any string that does not contain tabs or spaces is acceptable.

An XYZ file may contain either one of the following scenarios:

1. The file contains as many coordinates as the atoms that they are being read for: all coordinates will be read from the file following the same order as the atoms appear in the selection generated using the keywords listed in section 6. (Note that the order is guaranteed only if a single type of selection keyword is used one or more times, and not guaranteed when different types of selection keywords are used.)
2. The file contains more coordinates than needed, and it is assumed to contain coordinates for the entire system: only coordinates that match the numeric indices of the selected atoms are read, in order of increasing number.

XYZ-file coordinates are read directly by Colvars and stored internally as double-precision floating point numbers (unlike VMD's reader, which uses single precision).

PDB files may be used either as one of the available mechanisms to select atoms (see the atomsFile keyword), or more frequently to read reference coordinates for least-squares fit alignment (see the refPositionsFile keyword).

To select atoms via the atomsFile keyword, the option atomsFile is required, and atoms are selected based on either one of the following cases.

1. All atoms with a non-zero value of the corresponding column are selected.
2. If and only if atomsFile is provided, only atoms with a value of atomsCol equaling atomsColValue are selected. This can be useful to reuse the same PDB file for generating multiple selections.

To read coordinates via the refPositionsFile keyword, there are four possible scenarios.

1. The file contains as many coordinates as the atoms that they are being read for: all coordinates will be read from the file following the same order as the atoms appear in the selection generated using the keywords listed in section 6. (Note that the order is guaranteed only if a single type of selection keyword is used one or more times, and not guaranteed when different types of selection keywords are used.)
2. The file contains more coordinates than needed, and it is assumed to contain coordinates for the entire system: only coordinates that match the numeric indices of the selected atoms are read, in order of increasing number.
3. If the corresponding refPositionsCol keyword is specified, only positions with a non-zero value of the column refPositionsCol are read. This is particularly useful when all atoms were selected via atomsFile and atomsCol, which can then be the same as refPositionsCol for loading coordinates.
4. This is a special case of the previous point: if both refPositionsCol and refPositionsColValue are specified, only atoms for which the refPositionsCol column as the value refPositionsColValue are read.

Due to the fixed-precision PDB format, it is not recommended to use PDB files to read coordinates when precision is a concern, and the XYZ format (see 4.7.2) is recommended instead.

Many simulation methods and analysis tools write files that contain functions of the collective variables tabulated on a grid (e.g. potentials of mean force or multidimentional histograms) for the purpose of analyzing results. Such files are produced by ABF (7.2), metadynamics (7.4), multidimensional histograms (7.10), as well as any restraint with optional thermodynamic integration support (7.1).

In some cases, these files may also be read as input of a new simulation. Suitable input files for this purpose are typically generated as output files of previous simulations, or directly by the user in the specific case of ensemble-biased metadynamics (7.4.5). This section explains the “multicolumn" format used by these files. For a multidimensional function $f({\xi }_1$, ${\xi }_2$, …$)$ the multicolumn grid format is defined as follows:

Lines beginning with the character “#" are the header of the file. $N_{cv}$ is the number of collective variables sampled by the grid. For each variable ${\xi }_i$, $min\left({\xi }_i\right)$ is the lowest value sampled by the grid (i.e. the left-most boundary of the grid along ${\xi }_i$), $width\left({\xi }_i\right)$ is the width of each grid step along ${\xi }_i$, $npoints\left({\xi }_i\right)$ is the number of points and $periodic\left({\xi }_i\right)$ is a flag whose value is 1 or 0 depending on whether the grid is periodic along ${\xi }_i$. In most situations:

• $min\left({\xi }_i\right)$ is given by the lowerBoundary keyword of the variable ${\xi }_i$;
• $width\left({\xi }_i\right)$ is given by the width keyword;
• $npoints\left({\xi }_i\right)$ is calculated from the two above numbers and the upperBoundary keyword;
• $periodic\left({\xi }_i\right)$ is set to 1 if and only if ${\xi }_i$ is periodic and the grids' boundaries cover its period.

How the grid's boundaries affect the sequence of points depends on how the contents of the file were computed. In many cases, such as histograms and PMFs computed by metadynamics (7.4.5), the values of ${\xi }_i$ in the first few columns correspond to the midpoints of the corresponing bins, i.e. ${\xi }_1^1=min\left({\xi }_i\right)+width\left({\xi }_i\right)∕2$. However, there is a slightly different format in PMF files computed by ABF (7.2) or other biases that use thermodynamic integration (7.1). In these cases, it is free-energy gradients that are accumulated on an (npoints)-long grid along each variable $\xi$: after these gradients are integrated, the resulting PMF is discretized on a slightly larger grid with (npoints+1) points along $\xi$ (unless the interval is periodic). Therefore, the grid's outer edges extend by $width\left({\xi }_i\right)∕2$ above and below the specified boundaries, so that for instance $min\left({\xi }_i\right)$ in the header appears to be shifted back by $width\left({\xi }_i\right)∕2$ compared to what would be expected. Please keep this difference in mind when comparing PMFs computed by different methods.

After the header, the rest of the file contains values of the tabulated function $f({\xi }_1$, ${\xi }_2$, …${\xi }_{N_{cv}})$, one for each line. The first $N_{cv}$ columns contain values of ${\xi }_1$, ${\xi }_2$, …${\xi }_{N_{cv}}$ and the last column contains the value of the function $f$. Points are sorted in ascending order with the fastest-changing values at the right (“C-style" order). Each sweep of the right-most variable ${\xi }_{N_{cv}}$ is terminated by an empty line. For two dimensional grid files, this allows quick visualization by programs such as GNUplot.

Example 1: multicolumn text file for a one-dimensional histogram with lowerBoundary = 15, upperBoundary = 48 and width = 0.1.

Example 2: multicolumn text file for a two-dimensional histogram of two dihedral angles (periodic interval with 6${}^{\circ }$ bins):

The Colvars trajectory file (with a suffix .colvars.traj) is a plain text file (scientific notation with 14-digit precision) whose columns represent quantities such as colvar values, applied forces, or individual restraints' energies. Under most scenarios, plotting or analyzing this file is straightforward: for example, the following contains a variable “$A$" and the energy of a restraint “$rA$":

#       step   A                     E_rA
           0    1.42467449615693e+01  6.30982865292123e+02
         100    1.42282559728026e+01  6.20640585041317e+02
…

Occasionally, if the Colvars configuration is changed mid-run certain quantities may be added or removed, changing the column layout. Labels in comment lines can assist in such cases: for example, consider the trajectory above with the addition of a second variable, “$B$", after 10,000 steps:

#       step   A                     E_rA
           0    1.42467449615693e+01  6.30982865292123e+02
         100    1.42282559728026e+01  6.20640585041317e+02
…
#       step   A                     B                     E_rA              
       10000    1.38136915830229e+01  9.99574098859265e-01  4.11184644791030e+02
       10100    1.36437184346326e+01  9.99574091957314e-01  3.37726286543895e+02 

Analyzing the above file with standard tools is possible, but laborious: a convenience script is provided for this and related purposes. It may be used either as a command-line tool or as a Python module:

>>> from plot_colvars_traj import Colvars_traj
>>> traj = Colvars_traj('test.colvars.traj')
>>> print(traj['A'].steps, traj['A'].values)
[    0   100  ...  10000 10100] [14.246745 14.228256 ... 13.813692 13.643718]
>>> print(traj['B'].steps, traj['B'].values)
[10000 10100] [0.999574  0.9995741] 

A collective variable is defined by the keyword colvar followed by its configuration options contained within curly braces:

colvar {
  name xi
  $<$other options$>$
  function_name {
    $<$parameters$>$
    $<$atom selection$>$
  }
} 

There are multiple ways of defining a variable:

• The simplest and most common way way is using one of the precompiled functions (here called “components"), which are listed in section 5.1. For example, using the keyword rmsd (section 5.5.1) defines the variable as the root mean squared deviation (RMSD) of the selected atoms.
• A new variable may also be constructed as a linear or polynomial combination of the components listed in section 5.1 (see 5.16 for details).
• A user-defined mathematical function of the existing components (see list in section 5.1), or of the atomic coordinates directly (see the cartesian keyword in 5.8.1). The function is defined through the keyword customFunction (see 5.17 for details).
• A user-defined Tcl function of the existing components (see list in section 5.1), or of the atomic coordinates directly (see the cartesian keyword in 5.8.1). The function is provided by a separate Tcl script, and referenced through the keyword scriptedFunction (see 5.18 for details).

Choosing a component (function) is the only parameter strictly required to define a collective variable. It is also highly recommended to specify a name for the variable:

•   Keyword name$⟨$Name of this colvar$⟩$
  Context: colvar
  Acceptable values: string
  Default value: “colvar" + numeric id
  Description: The name is an unique case-sensitive string which allows the Colvars module to identify this colvar unambiguously; it is also used in the trajectory file to label to the columns corresponding to this colvar.

In this context, the function that computes a colvar is called a component. A component's choice and definition consists of including in the variable's configuration a keyword indicating the type of function (e.g. rmsd), followed by a definition block specifying the atoms involved (see 6) and any additional parameters (cutoffs, “reference" values, …). At least one component must be chosen to define a variable: if none of the keywords listed below is found, an error is raised.

The following components implement functions with a scalar value (i.e. a real number):

• distance: distance between two groups;
• distanceZ: projection of a distance vector on an axis;
• distanceXY: projection of a distance vector on a plane;
• distanceInv: mean distance between two groups of atoms (e.g. NOE-based distance);
• angle: angle between three groups;
• dihedral: torsional (dihedral) angle between four groups;
• dipoleAngle: angle between two groups and dipole of a third group;
• dipoleMagnitude: magnitude of the dipole of a group of atoms;
• polarTheta: polar angle of a group in spherical coordinates;
• polarPhi: azimuthal angle of a group in spherical coordinates;
• eulerPhi: Roll angle of rotation from references coordinates;
• eulerTheta: Pitch angle of rotation from references coordinates;
• eulerPsi: Yaw angle of rotation from references coordinates;
• coordNum: coordination number between two groups;
• selfCoordNum: coordination number of atoms within a group;
• hBond: hydrogen bond between two atoms;
• rmsd: root mean square deviation (RMSD) from a set of reference coordinates;
• eigenvector: projection of the atomic coordinates on a vector;
• mapTotal: total value of a volumetric map;
• orientationAngle: angle of the best-fit rotation from a set of reference coordinates;
• orientationProj: cosine of orientationProj;
• spinAngle: projection orthogonal to an axis of the best-fit rotation from a set of reference coordinates;
• tilt: projection on an axis of the best-fit rotation from a set of reference coordinates;
• gyration: radius of gyration of a group of atoms;
• inertia: moment of inertia of a group of atoms;
• inertiaZ: moment of inertia of a group of atoms around a chosen axis;
• alpha: $\alpha$-helix content of a protein segment.
• dihedralPC: projection of protein backbone dihedrals onto a dihedral principal component.

Some components do not return scalar, but vector values:

• distanceVec: distance vector between two groups (length: 3);
• distanceDir: unit vector parallel to distanceVec (length: 3);
• cartesian: vector of atomic Cartesian coordinates (length: $N$ times the number of Cartesian components requested, X, Y or Z);
• distancePairs: vector of mutual distances (length: $N_1\times N_2$);
• orientation: best-fit rotation, expressed as a unit quaternion (length: 4).

The types of components used in a colvar (scalar or not) determine the properties of that colvar, and particularly which biasing or analysis methods can be applied.

What if “X" is not listed? If a function type is not available on this list, it may be possible to define it as a polynomial superposition of existing ones (see 5.16), a custom function (see 5.17), or a scripted function (see 5.18).

In the rest of this section, all available component types are listed, along with their physical units and their ranges of values, if limited. Such ranges are often used to define automatically default sampling intervals, for example by setting the parameters lowerBoundary and upperBoundary in the parent colvar.

For each type of component, the available configurations keywords are listed: when two components share certain keywords, the second component references to the documentation of the first one that uses that keyword. The very few keywords that are available for all types of components are listed in a separate section 5.13.

The distance {...} block defines a distance component between the two atom groups, group1 and group2.

List of keywords (see also 5.16 for additional options):

•   Keyword group1$⟨$First group of atoms$⟩$
  Context: distance
  Acceptable values: Block group1 {...}
  Description: First group of atoms.
•   group2: analogous to group1
•   Keyword forceNoPBC$⟨$Calculate absolute rather than minimum-image distance?$⟩$
  Context: distance
  Acceptable values: boolean
  Default value: no
  Description: By default, in calculations with periodic boundary conditions, the distance component returns the distance according to the minimum-image convention. If this parameter is set to yes, PBC will be ignored and the distance between the coordinates as maintained internally will be used. This is only useful in a limited number of special cases, e.g. to describe the distance between remote points of a single macromolecule, which cannot be split across periodic cell boundaries, and for which the minimum-image distance might give the wrong result because of a relatively small periodic cell.
•   Keyword oneSiteTotalForce$⟨$Measure total force on group 1 only?$⟩$
  Context: angle, dipoleAngle, dihedral
  Acceptable values: boolean
  Default value: no
  Description: If this is set to yes, the total force is measured along a vector field (see equation (28) in section 7.2) that only involves atoms of group1. This option is only useful for ABF, or custom biases that compute total forces. See section 7.2 for details.

The value returned is a positive number (in length unit), ranging from $0$ to the largest possible interatomic distance within the chosen boundary conditions (with PBCs, the minimum image convention is used unless the forceNoPBC option is set).

The distanceZ {...} block defines a distance projection component, which can be seen as measuring the distance between two groups projected onto an axis, or the position of a group along such an axis. The axis can be defined using either one reference group and a constant vector, or dynamically based on two reference groups. One of the groups can be set to a dummy atom to allow the use of an absolute Cartesian coordinate.

List of keywords (see also 5.16 for additional options):

•   Keyword main$⟨$Main group of atoms$⟩$
  Context: distanceZ
  Acceptable values: Block main {...}
  Description: Group of atoms whose position $r$ is measured.
•   Keyword ref$⟨$Reference group of atoms$⟩$
  Context: distanceZ
  Acceptable values: Block ref {...}
  Description: Reference group of atoms. The position of its center of mass is noted $r_1$ below.
•   Keyword ref2$⟨$Secondary reference group$⟩$
  Context: distanceZ
  Acceptable values: Block ref2 {...}
  Default value: none
  Description: Optional group of reference atoms, whose position $r_2$ can be used to define a dynamic projection axis: $e={(\parallel r_2-r_1\parallel )}^{-1}\times (r_2-r_1)$. In this case, the origin is $r_m=1∕2(r_1+r_2)$, and the value of the component is $e\cdot (r-r_m)$.
•   Keyword axis$⟨$Projection axis$⟩$
  Context: distanceZ
  Acceptable values: (x, y, z) triplet
  Default value: (0.0, 0.0, 1.0)
  Description: This vector will be normalized to define a projection axis $e$ for the distance vector $r-r_1$ joining the centers of groups ref and main. The value of the component is then $e\cdot (r-r_1)$. The vector should be written as three components separated by commas and enclosed in parentheses.
• Keyword forceNoPBC: see definition of forceNoPBC (distance component)
• Keyword oneSiteTotalForce: see definition of oneSiteTotalForce (distance component)

This component returns a number (in length unit) whose range is determined by the chosen boundary conditions. For instance, if the $z$ axis is used in a simulation with periodic boundaries, the returned value ranges between $-b_z∕2$ and $b_z∕2$, where $b_z$ is the box length along $z$ (this behavior is disabled if forceNoPBC is set).

The distanceXY {...} block defines a distance projected on a plane, and accepts the same keywords as the component distanceZ, i.e. main, ref, either ref2 or axis, and oneSiteTotalForce. It returns the norm of the projection of the distance vector between main and ref onto the plane orthogonal to the axis. The axis is defined using the axis parameter or as the vector joining ref and ref2 (see distanceZ above).

List of keywords (see also 5.16 for additional options):

• Keyword main: see definition of main (distanceZ component)
• Keyword ref: see definition of ref (distanceZ component)
• Keyword ref2: see definition of ref2 (distanceZ component)
• Keyword axis: see definition of axis (distanceZ component)
• Keyword forceNoPBC: see definition of forceNoPBC (distance component)
• Keyword oneSiteTotalForce: see definition of oneSiteTotalForce (distance component)

The distanceVec {...} block defines a distance vector component, which accepts the same keywords as the component distance: group1, group2, and forceNoPBC. Its value is the 3-vector joining the centers of mass of group1 and group2.

List of keywords (see also 5.16 for additional options):

• Keyword group1: see definition of group1 (distance component)
• group2: analogous to group1
• Keyword forceNoPBC: see definition of forceNoPBC (distance component)
• Keyword oneSiteTotalForce: see definition of oneSiteTotalForce (distance component)

The distanceDir {...} block defines a distance unit vector component, which accepts the same keywords as the component distance: group1, group2, and forceNoPBC. It returns a 3-dimensional unit vector $d=(d_x,d_y,d_z)$, with $\left|d\right|=1$.

List of keywords (see also 5.16 for additional options):

• Keyword group1: see definition of group1 (distance component)
• group2: analogous to group1
• Keyword forceNoPBC: see definition of forceNoPBC (distance component)
• Keyword oneSiteTotalForce: see definition of oneSiteTotalForce (distance component)

The distanceInv {...} block defines a generalized mean distance between two groups of atoms 1 and 2, where each distance is taken to the power $-n$:

where $d_{ij}$ is the distance between atoms $i$ and $j$ in groups 1 and 2 respectively, and $n$ is an even integer.

List of keywords (see also 5.16 for additional options):

• Keyword group1: see definition of group1 (distance component)
• group2: analogous to group1
• Keyword oneSiteTotalForce: see definition of oneSiteTotalForce (distance component)
• Keyword exponent$⟨$Exponent $n$ in equation 2$⟩$
  Context: distanceInv
  Acceptable values: positive even integer
  Default value: 6
  Description: Defines the exponent to which the individual distances are elevated before averaging. The default value of 6 is useful for example to applying restraints based on NOE-measured distances.

This component returns a number ranging from $0$ to the largest possible distance within the chosen boundary conditions.

The angle {...} block defines an angle, and contains the three blocks group1, group2 and group3, defining the three groups. It returns an angle (in degrees) within the interval $[0:180]$.

List of keywords (see also 5.16 for additional options):

• Keyword group1: see definition of group1 (distance component)
• group2: analogous to group1
• group3: analogous to group1
• Keyword forceNoPBC: see definition of forceNoPBC (distance component)
• Keyword oneSiteTotalForce: see definition of oneSiteTotalForce (distance component)

The dipoleAngle {...} block defines an angle, and contains the three blocks group1, group2 and group3, defining the three groups, being group1 the group where dipole is calculated. It returns an angle (in degrees) within the interval $[0:180]$.

List of keywords (see also 5.16 for additional options):

• Keyword group1: see definition of group1 (distance component)
• group2: analogous to group1
• group3: analogous to group1
• Keyword forceNoPBC: see definition of forceNoPBC (distance component)
• Keyword oneSiteTotalForce: see definition of oneSiteTotalForce (distance component)

The dihedral {...} block defines a torsional angle, and contains the blocks group1, group2, group3 and group4, defining the four groups. It returns an angle (in degrees) within the interval $[-180:180]$. The Colvars module calculates all the distances between two angles taking into account periodicity. For instance, reference values for restraints or range boundaries can be defined by using any real number of choice.

List of keywords (see also 5.16 for additional options):

• Keyword group1: see definition of group1 (distance component)
• group2: analogous to group1
• group3: analogous to group1
• group4: analogous to group1
• Keyword forceNoPBC: see definition of forceNoPBC (distance component)
• Keyword oneSiteTotalForce: see definition of oneSiteTotalForce (distance component)

The polarTheta {...} block defines the polar angle in spherical coordinates, for the center of mass of a group of atoms described by the block atoms. It returns an angle (in degrees) within the interval $[0:180]$. To obtain spherical coordinates in a frame of reference tied to another group of atoms, use the fittingGroup (6.2) option within the atoms block. An example is provided in file examples/11_polar_angles.in of the Colvars public repository.

List of keywords (see also 5.16 for additional options):

•   Keyword atoms$⟨$Atom group$⟩$
  Context: polarPhi
  Acceptable values: atoms {...} block
  Description: Defines the group of atoms for the COM of which the angle should be calculated.

The polarPhi {...} block defines the azimuthal angle in spherical coordinates, for the center of mass of a group of atoms described by the block atoms. It returns an angle (in degrees) within the interval $[-180:180]$. The Colvars module calculates all the distances between two angles taking into account periodicity. For instance, reference values for restraints or range boundaries can be defined by using any real number of choice. To obtain spherical coordinates in a frame of reference tied to another group of atoms, use the fittingGroup (6.2) option within the atoms block. An example is provided in file examples/11_polar_angles.in of the Colvars public repository.

List of keywords (see also 5.16 for additional options):

•   Keyword atoms$⟨$Atom group$⟩$
  Context: polarPhi
  Acceptable values: atoms {...} block
  Description: Defines the group of atoms for the COM of which the angle should be calculated.

The coordNum {...} block defines a coordination number (or number of contacts), which calculates the function $(1-{(d∕d_0)}^n)∕(1-{(d∕d_0)}^m)$, where $d_0$ is the “cutoff" distance, and $n$ and $m$ are exponents that can control its long range behavior and stiffness [3]. This function is summed over all pairs of atoms in group1 and group2:

List of keywords (see also 5.16 for additional options):

•   Keyword group1: see definition of group1 (distance component)
•   group2: analogous to group1
•   Keyword cutoff$⟨$“Interaction" distance (length unit)$⟩$
  Context: coordNum
  Acceptable values: positive decimal
  Default value: 4.0 Å
  Description: This number defines the switching distance to define an interatomic contact: for $d\ll d_0$, the switching function $(1-{(d∕d_0)}^n)∕(1-{(d∕d_0)}^m)$ is close to 1, at $d=d_0$ it has a value of $n∕m$ ($1∕2$ with the default $n$ and $m$), and at $d\gg d_0$ it goes to zero approximately like $d^{m-n}$. Hence, for a proper behavior, $m$ must be larger than $n$.
•   Keyword cutoff3$⟨$Reference distance vector (length unit)$⟩$
  Context: coordNum
  Acceptable values: “(x, y, z)" triplet of positive decimals
  Default value: (4.0, 4.0, 4.0) 
  Description: The three components of this vector define three different cutoffs $d_0$ for each direction. This option is mutually exclusive with cutoff.
•   Keyword expNumer$⟨$Numerator exponent$⟩$
  Context: coordNum
  Acceptable values: positive even integer
  Default value: 6
  Description: This number defines the $n$ exponent for the switching function.
•   Keyword expDenom$⟨$Denominator exponent$⟩$
  Context: coordNum
  Acceptable values: positive even integer
  Default value: 12
  Description: This number defines the $m$ exponent for the switching function.
•   Keyword group2CenterOnly$⟨$Use only group2's center of mass$⟩$
  Context: coordNum
  Acceptable values: boolean
  Default value: off
  Description: If this option is on, only contacts between each atoms in group1 and the center of mass of group2 are calculated (by default, the sum extends over all pairs of atoms in group1 and group2). If group2 is a dummyAtom, this option is set to yes by default.
•   Keyword tolerance$⟨$Pairlist control$⟩$
  Context: coordNum
  Acceptable values: decimal
  Default value: 0.0
  Description: This controls the pairlist feature, dictating the minimum value for each summation element in Eq. 3 such that the pair that contributed the summation element is included in subsequent simulation timesteps until the next pairlist recalculation. For most applications, this value should be small (eg. 0.001) to avoid missing important contributions to the overall sum. Higher values will improve performance by reducing the number of pairs that contribute to the sum. Values above 1 will exclude all possible pair interactions. Similarly, values below 0 will never exclude a pair from consideration. To ensure continuous forces, Eq. 3 is further modified by subtracting the tolerance and then rescaling so that each pair covers the range $\left[0,1\right]$.
•   Keyword pairListFrequency$⟨$Pairlist regeneration frequency$⟩$
  Context: coordNum
  Acceptable values: positive integer
  Default value: 100
  Description: This controls the pairlist feature, dictating how many steps are taken between regenerating pairlists if the tolerance is greater than 0.

This component returns a dimensionless number, which ranges from approximately 0 (all interatomic distances are much larger than the cutoff) to $N_{group1}\times N_{group2}$ (all distances are less than the cutoff), or $N_{group1}$ if group2CenterOnly is used. For performance reasons, at least one of group1 and group2 should be of limited size or group2CenterOnly should be used: the cost of the loop over all pairs grows as $N_{group1}\times N_{group2}$. Setting $tolerance>0$ ameliorates this to some degree, although every pair is still checked to regenerate the pairlist.

The selfCoordNum {...} block defines a coordination number similarly to the component coordNum, but the function is summed over atom pairs within group1:

The keywords accepted by selfCoordNum are a subset of those accepted by coordNum, namely group1 (here defining all of the atoms to be considered), cutoff, expNumer, and expDenom.

List of keywords (see also 5.16 for additional options):

• Keyword group1: see definition of group1 (coordNum component)
• Keyword cutoff: see definition of cutoff (coordNum component)
• Keyword cutoff3: see definition of cutoff3 (coordNum component)
• Keyword expNumer: see definition of expNumer (coordNum component)
• Keyword expDenom: see definition of expDenom (coordNum component)
• Keyword tolerance: see definition of tolerance (coordNum component)
• Keyword pairListFrequency: see definition of pairListFrequency (coordNum component)

This component returns a dimensionless number, which ranges from approximately 0 (all interatomic distances much larger than the cutoff) to $N_{group1}\times (N_{group1}-1)∕2$ (all distances within the cutoff). For performance reasons, group1 should be of limited size, because the cost of the loop over all pairs grows as $N_{group1}^2$.

The hBond {...} block defines a hydrogen bond, implemented as a coordination number (eq. 3) between the donor and the acceptor atoms. Therefore, it accepts the same options cutoff (with a different default value of 3.3 Å), expNumer (with a default value of 6) and expDenom (with a default value of 8). Unlike coordNum, it requires two atom numbers, acceptor and donor, to be defined. It returns an adimensional number, with values between 0 (acceptor and donor far outside the cutoff distance) and 1 (acceptor and donor much closer than the cutoff).

List of keywords (see also 5.16 for additional options):

• Keyword acceptor$⟨$Number of the acceptor atom$⟩$
  Context: hBond
  Acceptable values: positive integer
  Description: Number that uses the same convention as atomNumbers.
• donor: analogous to acceptor
• Keyword cutoff: see definition of cutoff (coordNum component)
  Note: default value is 3.3 Å.
• Keyword expNumer: see definition of expNumer (coordNum component)
  Note: default value is 6.
• Keyword expDenom: see definition of expDenom (coordNum component)
  Note: default value is 8.

The block rmsd {...} defines the root mean square replacement (RMSD) of a group of atoms with respect to a reference structure. For each set of coordinates $\left\{x_1\right(t),x_2(t),\dots \&ApplyFunction;<!--FUNCTION\; APPLICATION-->x_N(t\left)\right\}$, the colvar component rmsd calculates the optimal rotation $U^{\left\{x_i\right(t\left)\right\}\to \left\{x_i^{\left(ref\right)}\right\}}$ that best superimposes the coordinates $\left\{x_i\right(t\left)\right\}$ onto a set of reference coordinates $\left\{x_i^{\left(ref\right)}\right\}$. Both the current and the reference coordinates are centered on their centers of geometry, $x_{cog}\left(t\right)$ and $x_{cog}^{\left(ref\right)}$. The root mean square displacement is then defined as:

The optimal rotation $U^{\left\{x_i\right(t\left)\right\}\to \left\{x_i^{\left(ref\right)}\right\}}$ is calculated within the formalism developed in reference [4], which guarantees a continuous dependence of $U^{\left\{x_i\right(t\left)\right\}\to \left\{x_i^{\left(ref\right)}\right\}}$ with respect to $\left\{x_i\right(t\left)\right\}$.

List of keywords (see also 5.16 for additional options):

•   Keyword atoms$⟨$Atom group$⟩$
  Context: rmsd
  Acceptable values: atoms {...} block
  Description: Defines the group of atoms of which the RMSD should be calculated. Optimal fit options (such as refPositions and rotateToReference) should typically NOT be set within this block. Exceptions to this rule are the special cases discussed in the Advanced usage paragraph below.
•   Keyword refPositions$⟨$Reference coordinates$⟩$
  Context: rmsd
  Acceptable values: space-separated list of (x, y, z) triplets
  Description: This option (mutually exclusive with refPositionsFile) sets the reference coordinates for RMSD calculation, and uses these to compute the roto-translational fit. See the equivalent option refPositions within the atom group definition for details on acceptable formats and other features.
•   Keyword refPositionsFile$⟨$Reference coordinates file$⟩$
  Context: rmsd
  Acceptable values: UNIX filename
  Description: This option (mutually exclusive with refPositions) sets the reference coordinates for RMSD calculation, and uses these to compute the roto-translational fit. See the equivalent option refPositionsFile within the atom group definition for details on acceptable file formats and other features.
•   Keyword refPositionsCol$⟨$PDB column containing atom flags$⟩$
  Context: rmsd
  Acceptable values: O, B, X, Y, or Z
  Description: If refPositionsFile is a PDB file that contains all the atoms in the topology, this option may be provided to set which PDB field is used to flag the reference coordinates for atoms.
•   Keyword refPositionsColValue$⟨$Atom selection flag in the PDB column$⟩$
  Context: rmsd
  Acceptable values: positive decimal
  Description: If defined, this value identifies in the PDB column refPositionsCol of the file refPositionsFile which atom positions are to be read. Otherwise, all positions with a non-zero value are read.
•   Keyword atomPermutation$⟨$Alternate ordering of atoms for RMSD computation$⟩$
  Context: rmsd
  Acceptable values: List of atom numbers
  Description: If defined, this parameter defines a re-ordering (permutation) of the 1-based atom numbers that can be used to compute the RMSD, typically due to molecular symmetry. This parameter can be specified multiple times, each one defining a new permutation: the returned RMSD value is the minimum over the set of permutations. For example, if the atoms making up the group are 6, 7, 8, 9, and atoms 7, 8, and 9 are invariant by circular permutation (as the hydrogens in a CH3 group), a symmetry-adapted RMSD would be obtained by adding:
  atomPermutation 6 8 9 7
  atomPermutation 6 9 7 8
  This will result in these 2 atom orders being considered in addition to the order used when defining the atom group. Note that this does not affect the least-squares roto-translational fit. Therefore, this feature is mostly useful when using custom fitting parameters within the atom group, such as fittingGroup, or when fitting is disabled altogether. For details, see reference [5].

This component returns a positive real number (in length unit).

1. applying the optimal translation, but no rotation (rotateToReference off), to bias or restrain the shape and orientation, but not the position of the atom group;
2. applying the optimal rotation, but no translation (centerToReference off), to bias or restrain the shape and position, but not the orientation of the atom group;
3. disabling the application of optimal roto-translations, which lets the RMSD component describe the deviation of atoms from fixed positions in the laboratory frame: this allows for custom positional restraints within the Colvars module;
4. fitting the atomic positions to different reference coordinates than those used in the RMSD calculation itself (by specifying refPositions or refPositionsFile within the atom group as well as within the rmsd block);
5. applying the optimal rotation and/or translation from a separate atom group, defined through fittingGroup: the RMSD then reflects the deviation from reference coordinates in a separate, moving reference frame (see example in the section on fittingGroup).

The block eigenvector {...} defines the projection of the coordinates of a group of atoms (or more precisely, their deviations from the reference coordinates) onto a vector in ${ℝ}^{3n}$, where $n$ is the number of atoms in the group. The computed quantity is the total projection:

where, as in the rmsd component, $U$ is the optimal rotation matrix, $x_{cog}\left(t\right)$ and $x_{cog}^{\left(ref\right)}$ are the centers of geometry of the current and reference positions respectively, and $v_i$ are the components of the vector for each atom. Example choices for $\left(v_i\right)$ are an eigenvector of the covariance matrix (essential mode), or a normal mode of the system. It is assumed that ${\sum \&ApplyFunction;<!--FUNCTION\; APPLICATION-->}_i{v}_i=0$: otherwise, the Colvars module centers the $v_i$ automatically when reading them from the configuration.

List of keywords (see also 5.16 for additional options):

• Keyword atoms: see definition of atoms (rmsd component)
• Keyword refPositions: see definition of refPositions (rmsd component)
• Keyword refPositionsFile: see definition of refPositionsFile (rmsd component)
• Keyword refPositionsCol: see definition of refPositionsCol (rmsd component)
• Keyword refPositionsColValue: see definition of refPositionsColValue (rmsd component)
• Keyword vector$⟨$Vector components$⟩$
  Context: eigenvector
  Acceptable values: space-separated list of (x, y, z) triplets
  Description: This option (mutually exclusive with vectorFile) sets the values of the vector components.
• Keyword vectorFile$⟨$file containing vector components$⟩$
  Context: eigenvector
  Acceptable values: UNIX filename
  Description: This option (mutually exclusive with vector) sets the name of an XYZ (4.7.3) or PDB coordinate file containing the vector components. For a PDB file specifically, the components are read from the X, Y and Z fields. Note: The PDB file has limited precision and fixed-point numbers: in some cases, the vector components may not be accurately represented; a XYZ file should be used instead, containing floating-point numbers. Note: Reading data from a coordinate file may entail an automatic unit conversion if the length unit currently used by the MD engine is not Å. If this is not the desired behavior, this can be remedied using the normalizeVectoroption described below.
• Keyword vectorCol$⟨$PDB column used to flag participating atoms$⟩$
  Context: eigenvector
  Acceptable values: O or B
  Description: Analogous to atomsCol.
• Keyword vectorColValue$⟨$Value used to flag participating atoms in the PDB file$⟩$
  Context: eigenvector
  Acceptable values: positive decimal
  Description: Analogous to atomsColValue.
• Keyword normalizeVector$⟨$Normalize the vector components when reading them?$⟩$
  Context: eigenvector
  Acceptable values: boolean
  Default value: off
  Description: If this flag is activated, the norm of the vector $\left|v\right|=\sqrt{{\sum \&ApplyFunction;<!--FUNCTION\; APPLICATION-->}_i{\left|v_i\right|}^2}$ is set equal to 1 by automatically rescaling all the components $v_i$; alternatively, the value of $\left|v\right|$ is printed.
• Keyword differenceVector$⟨$The $3n$-dimensional vector is the difference between vector and refPositions$⟩$
  Context: eigenvector
  Acceptable values: boolean
  Default value: off
  Description: If this option is on, the numbers provided by vector or vectorFile are interpreted as another set of positions, $x_i^{\prime }$: the vector $v_i$ is then defined as $v_i=\left(x_i^{\prime }-x_i^{\left(ref\right)}\right)$. This allows to conveniently define a colvar $\xi$ as a projection on the linear transformation between two sets of positions, “A" and “B". If this flag is on, the vector is normalized so that $\xi =0$ when the atoms are at the set of positions “A" and $\xi =1$ at the set of positions “B". Setting normalizeVectoron overrides this behavior.

The block gyration {...} defines the parameters for calculating the radius of gyration of a group of atomic positions $\left\{x_1\right(t),x_2(t),\dots \&ApplyFunction;<!--FUNCTION\; APPLICATION-->x_N(t\left)\right\}$ with respect to their center of geometry, $x_{cog}\left(t\right)$:

This component must contain one atoms {...} block to define the atom group, and returns a positive number, expressed in length unit.

List of keywords (see also 5.16 for additional options):

• Keyword atoms: see definition of atoms (rmsd component)

The block inertia {...} defines the parameters for calculating the total moment of inertia of a group of atomic positions $\left\{x_1\right(t),x_2(t),\dots \&ApplyFunction;<!--FUNCTION\; APPLICATION-->x_N(t\left)\right\}$ with respect to their center of geometry, $x_{cog}\left(t\right)$:

Note that all atomic masses are set to 1 for simplicity. This component must contain one atoms {...} block to define the atom group, and returns a positive number, expressed in length unit${}^2$.

List of keywords (see also 5.16 for additional options):

• Keyword atoms: see definition of atoms (rmsd component)

List of keywords (see also 5.16 for additional options):

• Keyword atoms: see definition of atoms (rmsd component)

The block inertiaZ {...} defines the parameters for calculating the component along the axis $e$ of the moment of inertia of a group of atomic positions $\left\{x_1\right(t),x_2(t),\dots \&ApplyFunction;<!--FUNCTION\; APPLICATION-->x_N(t\left)\right\}$ with respect to their center of geometry, $x_{cog}\left(t\right)$:

Note that all atomic masses are set to 1 for simplicity. This component must contain one atoms {...} block to define the atom group, and returns a positive number, expressed in length unit${}^2$.

List of keywords (see also 5.16 for additional options):

• Keyword atoms: see definition of atoms (rmsd component)
• Keyword axis$⟨$Projection axis$⟩$
  Context: inertiaZ
  Acceptable values: (x, y, z) triplet
  Default value: (0.0, 0.0, 1.0)
  Description: The three components of this vector define (when normalized) the projection axis $e$.

The variables discussed in this section quantify the rotations of macromolecules (or other quasi-rigid objects) from a given set of reference coordinates to the current coordinates. Such rotations are computed following the same method used for best-fit RMSDs (see rmsd and fittingGroup). The underlying mathematical formalism is described in reference [4], and the implementation in reference [1].

The first of the functions described is the orientation, which describes the full rotation as a unit quaternion $q=(q_0,q_1,q_2,q_3)$, i.e. 4 numbers with one constraint (3 degrees of freedom). The quaternion $q$ is one of only two representations that are both complete and accurate, the other being a $3\times 3$ unit matrix with 3 independent parameters. Although $q$ is used internally in the Colvars module for features such as the rmsd function and the fittingGroup option, its direct use as a collective variable is more difficult, and mostly limited to fixed or moving restraints.

The two functions orientationAngle and orientationProj, with the latter being the cosine of the former, represent the amplitude of the full rotation described by $q$, regardless of the direction of its axis. As one-dimensional scalar variables, both orientationAngle and orientationProj are a much reduced simplification of the full rotation. However, they can be used in a variety of methods including both restraints and PMF computations.

A slightly more complete parametrization is achieved by decomposing the full rotation into the two parameters, tilt and spinAngle. These quantify the amplitudes of two independent sub-rotations away from a certain axis $e$, and around the same axis $e$, respectively. The axis $e$ is chosen by the user, and is by default the Z axis: under that choice, tilt is equivalent to the sine of the Euler “pitch" angle $𝜃$, and spinAngle to the sum of the other two angles, $(\varphi +\psi )$. This parameterization is mathematically well defined for almost all full rotations, including small ones when the current coordinates are almost completely aligned with the reference ones. However, a mathematical singularity prevents using the spinAngle function near configurations where the value of tilt tilt is -1 (i.e. a -180${}^{\circ }$ rotation around an axis orthogonal to $e$). For these reasons, tilt and spinAngle are useful when the allowed rotations are known to have approximately the same axis, and differ only in the magnitude of the corresponding angle. In this use case, spinAngle measures the angle of the sub-rotation around the chosen axis $e$, whereas tilt measures the dot product between $e$ and the actual axis of the full rotation.

Lastly, the traditional Euler angles are also available as the functions eulerPhi, eulerTheta and eulerPsi. Altogether, these are sufficient to represent all three degrees of freedom of a full rotation. However, they also suffer from the potential “gimbal lock" problem, which emerges whenever $𝜃\simeq \pm 90^{\circ }$, which includes also the case where the full rotation is small. Under such conditions, the angles $\varphi$ and $\psi$ are both ill-defined and cannot be used as collective variables. For these reasons, it is highly recommmended that Euler angles are used only in simulations where their range of applicability is known ahead of time, and excludes configurations where $𝜃\simeq \pm 90^{\circ }$ altogether.

The block orientation {...} returns the same optimal rotation used in the rmsd component to superimpose the coordinates $\left\{x_i\right(t\left)\right\}$ onto a set of reference coordinates $\left\{x_i^{\left(ref\right)}\right\}$. Such component returns a four dimensional vector $q=(q_0,q_1,q_2,q_3)$, with ${\sum \&ApplyFunction;<!--FUNCTION\; APPLICATION-->}_i{q}_i^2=1$; this quaternion expresses the optimal rotation $\left\{x_i\right(t\left)\right\}\to \left\{x_i^{\left(ref\right)}\right\}$ according to the formalism in reference [4]. The quaternion $(q_0,q_1,q_2,q_3)$ can also be written as $\left(\cos \&ApplyFunction;<!--FUNCTION\; APPLICATION-->(𝜃∕2),\sin \&ApplyFunction;<!--FUNCTION\; APPLICATION-->(𝜃∕2)u\right)$, where $𝜃$ is the angle and $u$ the normalized axis of rotation; for example, a rotation of 90${}^{\circ }$ around the $z$ axis is expressed as “(0.707, 0.0, 0.0, 0.707)". The script quaternion2rmatrix.tcl provides Tcl functions for converting to and from a $4\times 4$ rotation matrix in a format suitable for usage in VMD.

As for the component rmsd, the available options are atoms, refPositionsFile, refPositionsCol and refPositionsColValue, and refPositions.

Note: refPositionsand refPositionsFile define the set of positions from which the optimal rotation is calculated, but this rotation is not applied to the coordinates of the atoms involved: it is used instead to define the variable itself.

List of keywords (see also 5.16 for additional options):

• Keyword atoms: see definition of atoms (rmsd component)
• Keyword refPositions: see definition of refPositions (rmsd component)
• Keyword refPositionsFile: see definition of refPositionsFile (rmsd component)
• Keyword refPositionsCol: see definition of refPositionsCol (rmsd component)
• Keyword refPositionsColValue: see definition of refPositionsColValue (rmsd component)
• Keyword closestToQuaternion$⟨$Reference rotation$⟩$
  Context: orientation
  Acceptable values: “(q0, q1, q2, q3)" quadruplet
  Default value: (1.0, 0.0, 0.0, 0.0) (“null" rotation)
  Description: Between the two equivalent quaternions $(q_0,q_1,q_2,q_3)$ and $(-q_0,-q_1,-q_2,-q_3)$, the closer to (1.0, 0.0, 0.0, 0.0) is chosen. This simplifies the visualization of the colvar trajectory when sampled values are a smaller subset of all possible rotations. Note: this only affects the output, never the dynamics.

Tip: stopping the rotation of a protein. To stop the rotation of an elongated macromolecule in solution (and use an anisotropic box to save water molecules), it is possible to define a colvar with an orientation component, and restrain it through the harmonic bias around the identity rotation, (1.0, 0.0, 0.0, 0.0). Only the overall orientation of the macromolecule is affected, and not its internal degrees of freedom. The user should also take care that the macromolecule is composed by a single chain, or disable wrapAll otherwise.

The block orientationAngle {...} accepts the same base options as the component orientation: atoms, refPositions, refPositionsFile, refPositionsCol and refPositionsColValue. The returned value is the angle of rotation $𝜃$ between the current and the reference positions. This angle is expressed in degrees within the range [0${}^{\circ }$:180${}^{\circ }$].

List of keywords (see also 5.16 for additional options):

• Keyword atoms: see definition of atoms (rmsd component)
• Keyword refPositions: see definition of refPositions (rmsd component)
• Keyword refPositionsFile: see definition of refPositionsFile (rmsd component)
• Keyword refPositionsCol: see definition of refPositionsCol (rmsd component)
• Keyword refPositionsColValue: see definition of refPositionsColValue (rmsd component)

The block orientationProj {...} accepts the same base options as the component orientation: atoms, refPositions, refPositionsFile, refPositionsCol and refPositionsColValue. The returned value is the cosine of the angle of rotation $𝜃$ between the current and the reference positions. The range of values is [-1:1].

List of keywords (see also 5.16 for additional options):

• Keyword atoms: see definition of atoms (rmsd component)
• Keyword refPositions: see definition of refPositions (rmsd component)
• Keyword refPositionsFile: see definition of refPositionsFile (rmsd component)
• Keyword refPositionsCol: see definition of refPositionsCol (rmsd component)
• Keyword refPositionsColValue: see definition of refPositionsColValue (rmsd component)

The complete rotation described by orientation can optionally be decomposed into two sub-rotations: one is a “spin" rotation around e, and the other a “tilt" rotation around an axis orthogonal to e. The component spinAngle measures the angle of the “spin" sub-rotation around e.

List of keywords (see also 5.16 for additional options):

• Keyword atoms: see definition of atoms (rmsd component)
• Keyword refPositions: see definition of refPositions (rmsd component)
• Keyword refPositionsFile: see definition of refPositionsFile (rmsd component)
• Keyword refPositionsCol: see definition of refPositionsCol (rmsd component)
• Keyword refPositionsColValue: see definition of refPositionsColValue (rmsd component)
•   Keyword axis$⟨$Special rotation axis$⟩$
  Context: tilt
  Acceptable values: (x, y, z) triplet
  Default value: (0.0, 0.0, 1.0)
  Description: The three components of this vector define (when normalized) the special rotation axis used to calculate the tilt and spinAngle components.

The component spinAngle returns an angle (in degrees) within the periodic interval $[-180:180]$.

Note: the value of spinAngle is a continuous function almost everywhere, with the exception of configurations with the corresponding “tilt" angle equal to 180${}^{\circ }$ (i.e. the tilt component is equal to $-1$): in those cases, spinAngle is undefined. If such configurations are expected, consider defining a tilt colvar using the same axis e, and restraining it with a lower wall away from $-1$.

The component tilt measures the cosine of the angle of the “tilt" sub-rotation, which combined with the “spin" sub-rotation provides the complete rotation of a group of atoms. The cosine of the tilt angle rather than the tilt angle itself is implemented, because the latter is unevenly distributed even for an isotropic system: consider as an analogy the angle $𝜃$ in the spherical coordinate system. The component tilt relies on the same options as spinAngle, including the definition of the axis e. The values of tilt are real numbers in the interval $[-1:1]$: the value $1$ represents an orientation fully parallel to e (tilt angle = 0${}^{\circ }$), and the value $-1$ represents an anti-parallel orientation.

List of keywords (see also 5.16 for additional options):

• Keyword atoms: see definition of atoms (rmsd component)
• Keyword refPositions: see definition of refPositions (rmsd component)
• Keyword refPositionsFile: see definition of refPositionsFile (rmsd component)
• Keyword refPositionsCol: see definition of refPositionsCol (rmsd component)
• Keyword refPositionsColValue: see definition of refPositionsColValue (rmsd component)
• Keyword axis: see definition of axis (spinAngle component)

Assuming the axes of the original frame are denoted as x, y, z and the axes of the rotated frame as X, Y, Z, the line of nodes, N, can be defined as the intersection of the plane xy and XY. The axis perpendicular to N and z is defined as P. In this case, as illustrated in the figure below, the complete rotation described by orientation can optionally be decomposed into three Euler angles:

• the “roll" angle $\varphi$, i.e. the rotation angle from the x axis to the N axis;
• the “pitch" angle $𝜃$, i.e. the rotation angle from the P axis to the Z axis, and
• the “yaw" angle $\psi$, i.e. the rotation angle from the N axis to the X axis.

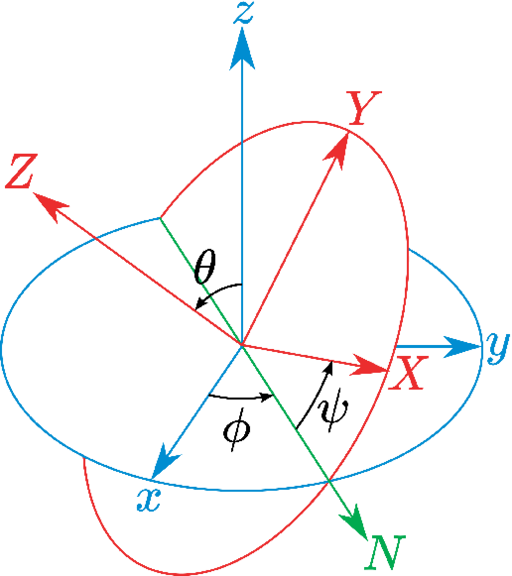
Although Euler angles are more straightforward to use than quaternions, they are also potentially subject to the “gimbal lock" problem:
https://en.wikipedia.org/wiki/Gimbal_lock
which arises whenever $𝜃\simeq \pm 90^{\circ }$, including the common case when the simulated coordinates are near the reference coordinates. Therefore, a safe use of Euler angles as collective variables requires the use of restraints to avoid such singularities, such as done in reference [6] and in the protein-ligand binding NAMD tutorial.

The eulerPhi component accepts exactly the same options as orientation, and measures the rotation angle from the x axis to the N axis. This angle is expressed in degrees within the periodic range $[-180^{\circ }:180^{\circ }]$.

List of keywords (see also 5.16 for additional options):

• Keyword atoms: see definition of atoms (rmsd component)
• Keyword refPositions: see definition of refPositions (rmsd component)
• Keyword refPositionsFile: see definition of refPositionsFile (rmsd component)

• Keyword refPositionsCol: see definition of refPositionsCol (rmsd component)

• Keyword refPositionsColValue: see definition of refPositionsColValue (rmsd component)

This component accepts exactly the same options as orientation, and measures the rotation angle from the P axis to the Z axis. This angle is expressed in degrees within the range $[-90^{\circ }:90^{\circ }]$.