colvars_gpu::rotation_derivative_gpu Struct Reference

Collaboration diagram for colvars_gpu::rotation_derivative_gpu:

Public Member Functions
	rotation_derivative_gpu ()
	Constructor. More...
int	init (const colvars_gpu::rotation_gpu *rot, const cvm::real *d_pos1, const cvm::real *d_pos2, const size_t num_atoms_pos1, const size_t num_atoms_pos2)
	Initialization of the rotation_derivative_gpu class. More...
int	add_prepare_derivative_nodes (rotation_derivative_dldq require_dl_dq, cudaGraph_t &graph, std::unordered_map< std::string, cudaGraphNode_t > &nodes_map)
	Add a "prepare_rotation_derivative" node to the CUDA graph. More...
template<bool use_dl, bool use_dq>
COLVARS_DEVICE void	calc_derivative_impl (const cvm::rvector(&ds)[4][4], cvm::rvector *_noalias const dl0_out, cvm::rvector *_noalias const dq0_out) const
	Actual implementation of the derivative calculation. More...
template<bool use_dl, bool use_dq>
COLVARS_DEVICE void	calc_derivative_wrt_group1 (int ia, cvm::rvector *_noalias const dl0_1_out, cvm::rvector *_noalias const dq0_1_out) const
	Calculate the derivatives of S, the leading eigenvalue L and the leading eigenvector Q with respect to m_pos1 More...
template<bool use_dl, bool use_dq>
COLVARS_DEVICE void	calc_derivative_wrt_group2 (int ia, cvm::rvector *_noalias const dl0_2_out, cvm::rvector *_noalias const dq0_2_out) const
	Calculate the derivatives of S, the leading eigenvalue L and the leading eigenvector Q with respect to m_pos2 More...
template<int i>
COLVARS_DEVICE cvm::rmatrix	project_force_to_C_from_dxdqi (cvm::real f_on_q) const
	Project the force on \(q_i\) (or the gradient of \(\frac{\mathrm{d}x}{\mathrm{d}q_i}\)) to the force on the correlation matrix \(C=\mathbf{r}_1^\intercal\mathbf{r}_2\), where \(\mathbf{r}_1\) and \(\mathbf{r}_2\) are \(N\times 3\) matrices containing the atom positions of atom group 1 and atom group 2 after centering on origin. More...
COLVARS_DEVICE cvm::rmatrix	project_force_to_C_from_dxdqi (int i, cvm::real f_on_q) const
template<typename dim4_array_t >
COLVARS_DEVICE cvm::rmatrix	project_force_to_C_from_dxdq (const dim4_array_t &sum_dxdq) const
	Project the force on \(\mathbf{q}\) (or the gradient of \(\frac{\mathrm{d}x}{\mathrm{d}q_i}\)) to the force on the correlation matrix \(C=\mathbf{r}_1^\intercal\mathbf{r}_2\), where \(\mathbf{r}_1\) and \(\mathbf{r}_2\) are \(N\times 3\) matrices containing the atom positions of atom group 1 and atom group 2 after centering on origin. More...
COLVARS_DEVICE cvm::rvector	project_force_to_group1 (size_t ia, const cvm::rmatrix &dxdC) const
	Project the force on the correlation matrix \(C\) to \(\mathbf{r}_1\). More...
COLVARS_DEVICE cvm::rvector	project_force_to_group2 (size_t ia, const cvm::rmatrix &dxdC) const
	Project the force on the correlation matrix \(C\) to \(\mathbf{r}_2\). More...

Public Attributes
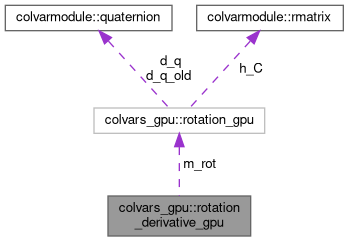
const colvars_gpu::rotation_gpu *	m_rot
	Reference to the rotation.
const cvm::real *	d_pos1x
	Reference to the atom positions of group 1.
const cvm::real *	d_pos1y
const cvm::real *	d_pos1z
const cvm::real *	d_pos2x
	Reference to the atom positions of group 2.
const cvm::real *	d_pos2y
const cvm::real *	d_pos2z
size_t	m_num_atoms_pos1
	Number of atoms in group1 (used in SOA)
size_t	m_num_atoms_pos2
	Number of atoms in group1 (used in SOA)
cvm::real *	tmp_Q0Q0
	GPU temporary variable that will be updated if prepare_derivative called.
cvm::real *	tmp_Q0Q0_L

Constructor & Destructor Documentation

rotation_derivative_gpu()

colvars_gpu::rotation_derivative_gpu::rotation_derivative_gpu

(

)

Constructor.

The object of this class is expected to be constructed on host-pinned memory.

Member Function Documentation

add_prepare_derivative_nodes()

int colvars_gpu::rotation_derivative_gpu::add_prepare_derivative_nodes	(	rotation_derivative_dldq	require_dl_dq,
		cudaGraph_t &	graph,
		std::unordered_map< std::string, cudaGraphNode_t > &	nodes_map
	)

Add a "prepare_rotation_derivative" node to the CUDA graph.

Parameters

[in]	require_dl_dq	Require the calculation of the derivatives of L or/and Q with respect to atoms.
[in]	graph	The CUDA graph where the node would be added
[out]	nodes_map	A map from operation names to cudaGraphNode_t for dependency lookup. A node termed as "prepare_rotation_derivative" would be added into the nodes_map.

Returns

COLVARS_OK if success and COLVARS_ERROR otherwise

The corresponding graph must be executed before calc_derivative_wrt_group1 and calc_derivative_wrt_group2 in order to prepare the tmp_Q0Q0 and tmp_Q0Q0_L.

calc_derivative_impl()

template<bool use_dl, bool use_dq>

COLVARS_DEVICE void colvars_gpu::rotation_derivative_gpu::calc_derivative_impl ( const cvm::rvector(&)  ds[4][4], cvm::rvector *_noalias const  dl0_out, cvm::rvector *_noalias const  dq0_out  ) const

inline

Actual implementation of the derivative calculation.

Parameters

[in]	ds	The derivative of matrix S with respect to an atom of either group 1 or group 2
[out]	dl0_out	The output of derivative of L
[out]	dq0_out	The output of derivative of Q

calc_derivative_wrt_group1()

template<bool use_dl, bool use_dq>

COLVARS_DEVICE void colvars_gpu::rotation_derivative_gpu::calc_derivative_wrt_group1 ( int  ia, cvm::rvector *_noalias const  dl0_1_out, cvm::rvector *_noalias const  dq0_1_out  ) const

inline

Calculate the derivatives of S, the leading eigenvalue L and the leading eigenvector Q with respect to m_pos1

Parameters

[in]	ia	The index the of atom
[out]	dl0_1_out	The output of derivative of L with respect to ia-th atom of group 1
[out]	dq0_1_out	The output of derivative of Q with respect to ia-th atom of group 1

calc_derivative_wrt_group2()

template<bool use_dl, bool use_dq>

COLVARS_DEVICE void colvars_gpu::rotation_derivative_gpu::calc_derivative_wrt_group2 ( int  ia, cvm::rvector *_noalias const  dl0_2_out, cvm::rvector *_noalias const  dq0_2_out  ) const

inline

Calculate the derivatives of S, the leading eigenvalue L and the leading eigenvector Q with respect to m_pos2

Parameters

[in]	ia	The index the of atom
[out]	dl0_2_out	The output of derivative of L with respect to ia-th atom of group 2
[out]	dq0_2_out	The output of derivative of Q with respect to ia-th atom of group 2

init()

int colvars_gpu::rotation_derivative_gpu::init	(	const colvars_gpu::rotation_gpu *	rot,
		const cvm::real *	d_pos1,
		const cvm::real *	d_pos2,
		const size_t	num_atoms_pos1,
		const size_t	num_atoms_pos2
	)

Initialization of the rotation_derivative_gpu class.

Parameters

[in]	rot	The colvars_gpu::rotation_gpu object
[in]	pos1	The atom positions of group 1
[in]	pos2	The atom positions of group 2
[in]	num_atoms_pos1	The number of atoms in group1
[in]	num_atoms_pos2	The number of atoms in group2

project_force_to_C_from_dxdq()

template<typename dim4_array_t >

COLVARS_DEVICE cvm::rmatrix colvars_gpu::rotation_derivative_gpu::project_force_to_C_from_dxdq ( const dim4_array_t &  sum_dxdq ) const

inline

Project the force on \(\mathbf{q}\) (or the gradient of \(\frac{\mathrm{d}x}{\mathrm{d}q_i}\)) to the force on the correlation matrix \(C=\mathbf{r}_1^\intercal\mathbf{r}_2\), where \(\mathbf{r}_1\) and \(\mathbf{r}_2\) are \(N\times 3\) matrices containing the atom positions of atom group 1 and atom group 2 after centering on origin.

See also project_force_to_C_from_dxdqi().

Template Parameters

dim4_array_t

The type of force acting on \(\mathbf{q}\).

Parameters

[in]

sum_dxdq

The force on \(\mathbf{q}\) or the gradient vector \((\frac{\mathrm{d}x}{\mathrm{d}q_0}, \frac{\mathrm{d}x}{\mathrm{d}q_1}, \frac{\mathrm{d}x}{\mathrm{d}q_2}, \frac{\mathrm{d}x}{\mathrm{d}q_3})\).

Returns

A 3x3 matrix. The matrix element at row \(j\) and column \(k\) is \(\sum_{i=0}^3 f_{q_i}\frac{\mathrm{d}q_i}{\mathrm{d}C_{jk}}\).

project_force_to_C_from_dxdqi()

template<int i>

COLVARS_DEVICE cvm::rmatrix colvars_gpu::rotation_derivative_gpu::project_force_to_C_from_dxdqi ( cvm::real  f_on_q ) const

inline

Project the force on \(q_i\) (or the gradient of \(\frac{\mathrm{d}x}{\mathrm{d}q_i}\)) to the force on the correlation matrix \(C=\mathbf{r}_1^\intercal\mathbf{r}_2\), where \(\mathbf{r}_1\) and \(\mathbf{r}_2\) are \(N\times 3\) matrices containing the atom positions of atom group 1 and atom group 2 after centering on origin.

This function can be only called after prepare_derivative(rotation_derivative_dldq::use_dq). It mulitplies the input with \(\frac{\mathrm{d}q_i}{\mathrm{d}C}\).

Template Parameters

i	The i-th component of the quaternion, must be in the range [0, 3]

Parameters

[in]

f_on_q

The force on \(q_i\) or the gradient of \(\frac{\mathrm{d}x}{\mathrm{d}q_i}\)

Returns

A 3x3 matrix. The matrix element at row \(j\) and column \(k\) is \(f_{q_i}\frac{\mathrm{d}q_i}{\mathrm{d}C_{jk}}\).

project_force_to_group1()

COLVARS_DEVICE cvm::rvector colvars_gpu::rotation_derivative_gpu::project_force_to_group1 ( size_t  ia, const cvm::rmatrix &  dxdC  ) const

inline

Project the force on the correlation matrix \(C\) to \(\mathbf{r}_1\).

Let \(C=\mathbf{r}_1^\intercal\mathbf{r}_2\), and the force on \(C\) be \(F_{C}\). This function returns the force on the i-th atom of \(\mathbf{r}_1\).

Parameters

[in]	ia	The atom index of the i-th atom in \(\mathbf{r}_1\)
[in]	dxdC	The 3x3 matrix containing the forces on each element of \(C\)

Returns

The force on the i-th atom of \(\mathbf{r}_1\)

project_force_to_group2()

COLVARS_DEVICE cvm::rvector colvars_gpu::rotation_derivative_gpu::project_force_to_group2 ( size_t  ia, const cvm::rmatrix &  dxdC  ) const

inline

Project the force on the correlation matrix \(C\) to \(\mathbf{r}_2\).

Let \(C=\mathbf{r}_1^\intercal\mathbf{r}_2\), and the force on \(C\) be \(F_{C}\). This function returns the force on the i-th atom of \(\mathbf{r}_2\).

Parameters

[in]	ia	The atom index of the i-th atom in \(\mathbf{r}_2\)
[in]	dxdC	The 3x3 matrix containing the forces on each element of \(C\)

Returns

The force on the i-th atom of \(\mathbf{r}_2\)

---

The documentation for this struct was generated from the following files:

• colvar_rotation_derivative.h
• colvar_rotation_derivative.cpp